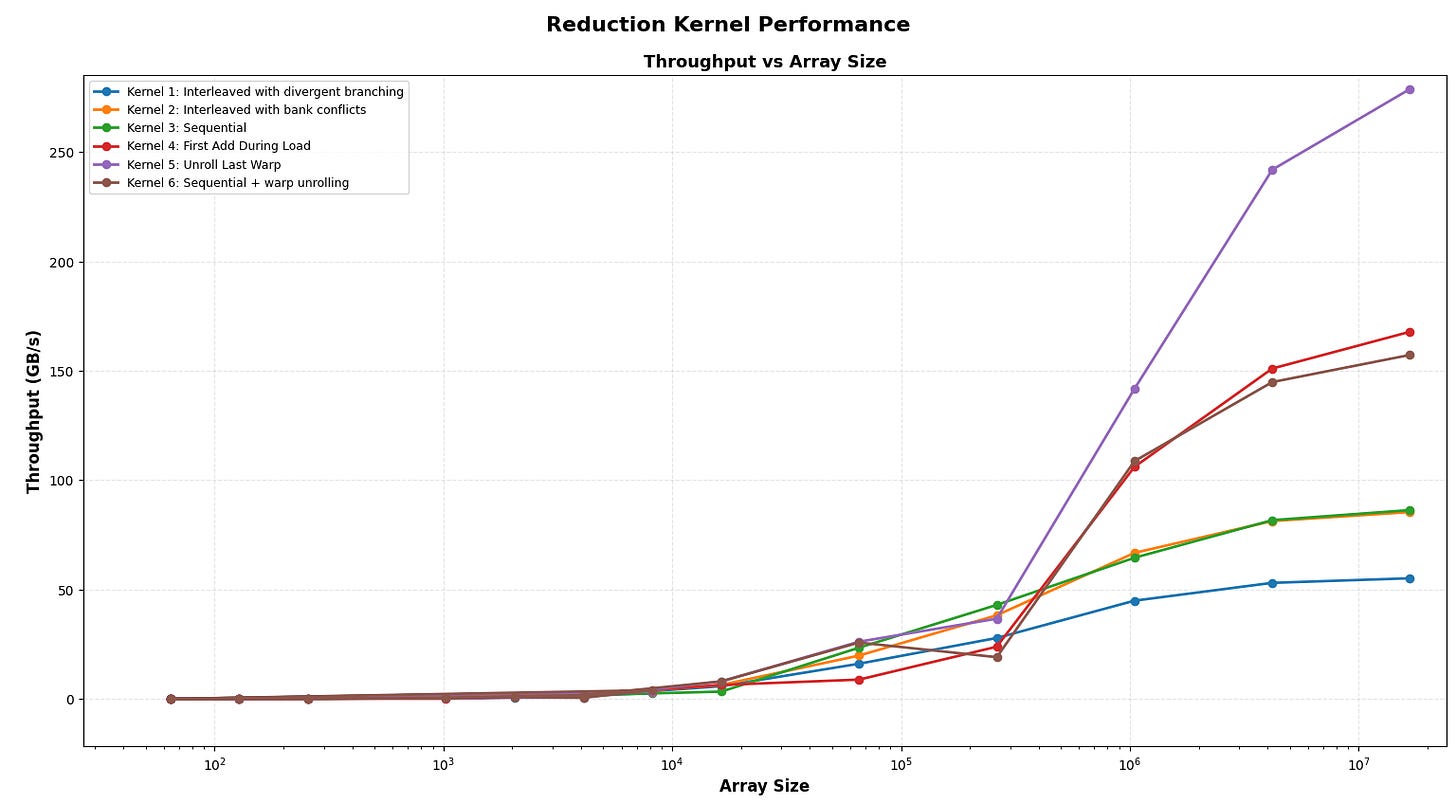
WorkLog: Reduction in CUDA

In this post, I’ll explore various methods to optimize Reductions in CUDA, mainly focus on Sum Reduction.

• GPU Used: RTX3060

• Code can be found at: Reduction in CUDA

Background

Reductions in programming refer to a pattern where we take multiple input values in order to get a single output using some operations.

Typical Reduction operations:

• Sum of all elements

• Minimum/Maximum

• Logical AND/OR etc.

Why Reductions are tricky in CUDA?

1. Serialization Problem

   A classical, single-threaded CPU reduction in a simple loop:

int sum = 0;
for (int i = 0; i < N; i++) {
    sum += array[i]; // fundamentally sequential!
}

This loop is fundamentally sequential: each iteration depends on the previous one.

On a GPU, however:

• Thousands of threads run concurrently

• Cannot all update the same variable (race condition)

  • CUDA has no hardware mechanism to synchronize all blocks at once while a kernel is running

2. Coordination Problem

GPUs have a hierarchical execution model:

1. Intra-block communication

   Threads can:

   • Communicate using shared memory

   • Synchronize using __syncthreads()

   This makes intra-block reduction efficient.

2. Inter-block communication

There is no built-in synchronization inside a single kernel. So combining partial results from different blocks is tricky.

There are largely two ways of approaching them, both with their pros and cons.

• Global Memory + Multiple Kernel Launches

• Atomic Operations to Global Memory

3. Memory Bandwidth Problem

A reduction has very low arithmetic intensity (AI):

• FLOPs ≈ N

• Bytes read ≈ 4N (for float)

• AI ≈ 1 FLOP per 4 bytes → extremely low

This means the reduction is memory-bound, not compute-bound. So, GPU cores sit idle because reduction is limited by memory bandwidth, not compute throughput.

Kernel 1: Interleaved Addressing(Naive method)

__global__ void reduction(const float* input, float* output, int N){
    extern __shared__ float sOut[];
    int tid = threadIdx.x;
    int gid = blockDim.x * blockIdx.x + threadIdx.x;

    sOut[tid] = (gid < N) ? input[gid] : 0.0f;
    __syncthreads();

    for(int i = 1;i < blockDim.x;i<<=1){
        if(tid % (2*i) == 0){
            sOut[tid] += sOut[tid + i];
        }
        __syncthreads();
    }
    if(tid == 0){
        output[blockIdx.x] = sOut[0];
    }
}

Issues with the above approach:

• modulo(%) operator is slow.

• Highly divergent and warps are very inefficient

  • Inside a warp(32 threads), the condition

    • if(tid % (2*i)==0)

  • activates only some threads based on modulus patterns

    • Example with i = 1:

      • Threads 0,2,4,6,… do work

      • Threads 1,3,5,7,… do nothing

    • This means exactly half the threads in every warp take the “true” branch and half take the “false” branch.

    • classic warp divergence.

• Possible out-of-bounds read: When tid + i >= blockDim.x, this will illegally read shared memory.

Kernel 2: Interleaved Addressing v2

Improvements over Kernel 1:

• Only 1 thread per pair performs work → no divergence pattern.

• No out-of-bounds because index + i < blockDim.x is guaranteed whenever index < blockDim.x.

__global__ void reduction(const float* input, float* output, int N){
    extern __shared__ float sOut[];
    int tid = threadIdx.x;
    int gid = blockDim.x * blockIdx.x + threadIdx.x;

    sOut[tid] = (gid < N) ? input[gid] : 0.0f;
    __syncthreads();

    for(int i = 1;i < blockDim.x;i *= 2){
        int index = 2 * i * tid;
        if(index < blockDim.x){
            sOut[index] += sOut[index + i];
        }
        __syncthreads();
    }

    if(tid == 0){
        output[blockIdx.x] = sOut[0];
    }
}

Issues with the above approach:

• Shared Memory bank conflict

  • occur when multiple threads attempt to access data from the same memory bank simultaneously.

  • These bank conflicts lead to serialization of what could otherwise be parallel memory accesses.

Kernel 3: Sequential Addressing

Advantages over the previous kernels:

• Better memory access pattern

  • Threads in a warp access consecutive elements for sout[tid] and sout[tid + i]

  • Less bank conflict in shared memory

__global__ void reduction(const float* input, float* output, int N){
    extern __shared__ float sout[];
    int tid = threadIdx.x;
    int gid = blockDim.x * blockIdx.x + threadIdx.x;

    // Load data into shared memory
    if(gid < N){
        sout[tid] = input[gid];
    }
    else{
        sout[tid] = 0.0f;
    }
    __syncthreads();

    // Parallel reduction within block
    for (int i = blockDim.x / 2; i > 0; i >>= 1) {
        if (tid < i) {
            sout[tid] += sout[tid + i];
        }
        __syncthreads();
    }

    // Write block result to global memory
    if(tid == 0){
        output[blockIdx.x] = sout[0];
    }
}

Issues:

• Warp underutilization

Kernel 4: First add during global load

Advantages:

• Fewer threads per block needed

  • Each thread handles two elements, so the active thread count for reduction is halved.

• Better global memory efficiency

  • Each thread reads two consecutive elements → better coalesced memory access.

  • Fewer threads → less shared-memory overhead.

__global__ void reduction(const float* input, float* output, int N){
    extern __shared__ float sOut[];
    int tid = threadIdx.x;
    int gid = 2 * blockDim.x * blockIdx.x + threadIdx.x;


    // Load two elements per thread if within bounds
    sOut[tid] = (gid < N ? input[gid] : 0.0f) 
        + (gid + blockDim.x < N ? input[gid + blockDim.x] : 0.0f);

    __syncthreads();

    for(int i = blockDim.x / 2;i > 0;i >>=1){
        if(tid < i){
            sOut[tid] += sOut[tid + i];
        }
        __syncthreads();
    }

    if(tid == 0){
        output[blockIdx.x] = sOut[0];
    }
}

Kernel 5: Unroll the last warp(Warp Optimization)

Advantages:

• Eliminates unnecessary synchronization for last warp

  • Synchronization is costly; skipping it reduces latency.

  • Accessing shared memory in a warp does not require synchronization.

  • volatile float* ensures the compiler doesn’t cache sdata[tid] in a register, so each read sees updated shared memory values.

__device__ void warpReduce(volatile float* sdata, int tid) {
sdata[tid] += sdata[tid + 32];
sdata[tid] += sdata[tid + 16];
sdata[tid] += sdata[tid + 8];
sdata[tid] += sdata[tid + 4];
sdata[tid] += sdata[tid + 2];
sdata[tid] += sdata[tid + 1];
}


__global__ void reduction(const float* input, float* output, int N){
    extern __shared__ float sOut[];
    int tid = threadIdx.x;
    int gid = blockDim.x * blockIdx.x + threadIdx.x;

    sOut[tid] = (gid < N) ? input[gid] : 0.0f;
    __syncthreads();

    for(int i = blockDim.x / 2;i > 32;i >>=1){
        if(tid < i){
            sOut[tid] += sOut[tid + i];
        }
        __syncthreads();
    }
    if(tid < 32){
        warpReduce(sOut,tid);
    }

    if(tid == 0){
        output[blockIdx.x] = sOut[0];
    }
}

Kernel 6: Sequential Addressing with warp-level Optimization

Advantages over Kernel 3:

• Utilizes warps which reduces thread synchronizations thus improving performance.

__global__ void reduction_6(const float* input, float* output, int N){
    extern __shared__ float sout[];
    int tid = threadIdx.x;
    int gid = blockDim.x * blockIdx.x + threadIdx.x;

    // Load data into shared memory
    if(gid < N){
        sout[tid] = input[gid];
    }
    else{
        sout[tid] = 0.0f;
    }
    __syncthreads();

    // Parallel reduction within block
    for (int i = blockDim.x / 2; i > 32; i >>= 1) {
        if (tid < i) {
            sout[tid] += sout[tid + i];
        }
        __syncthreads();
    }
    
    if(tid < 32){
        warpReduce(sout,tid);
    }

    // Write block result to global memory
    if(tid == 0){
        output[blockIdx.x] = sout[0];
    }
}

Benchmarking Results

References

• Optimizing Parallel Reduction in CUDA

• GPU Mode Lecture 9: Reductions